PROJECT MANAGEMENT
Achieve better profitability in your projects
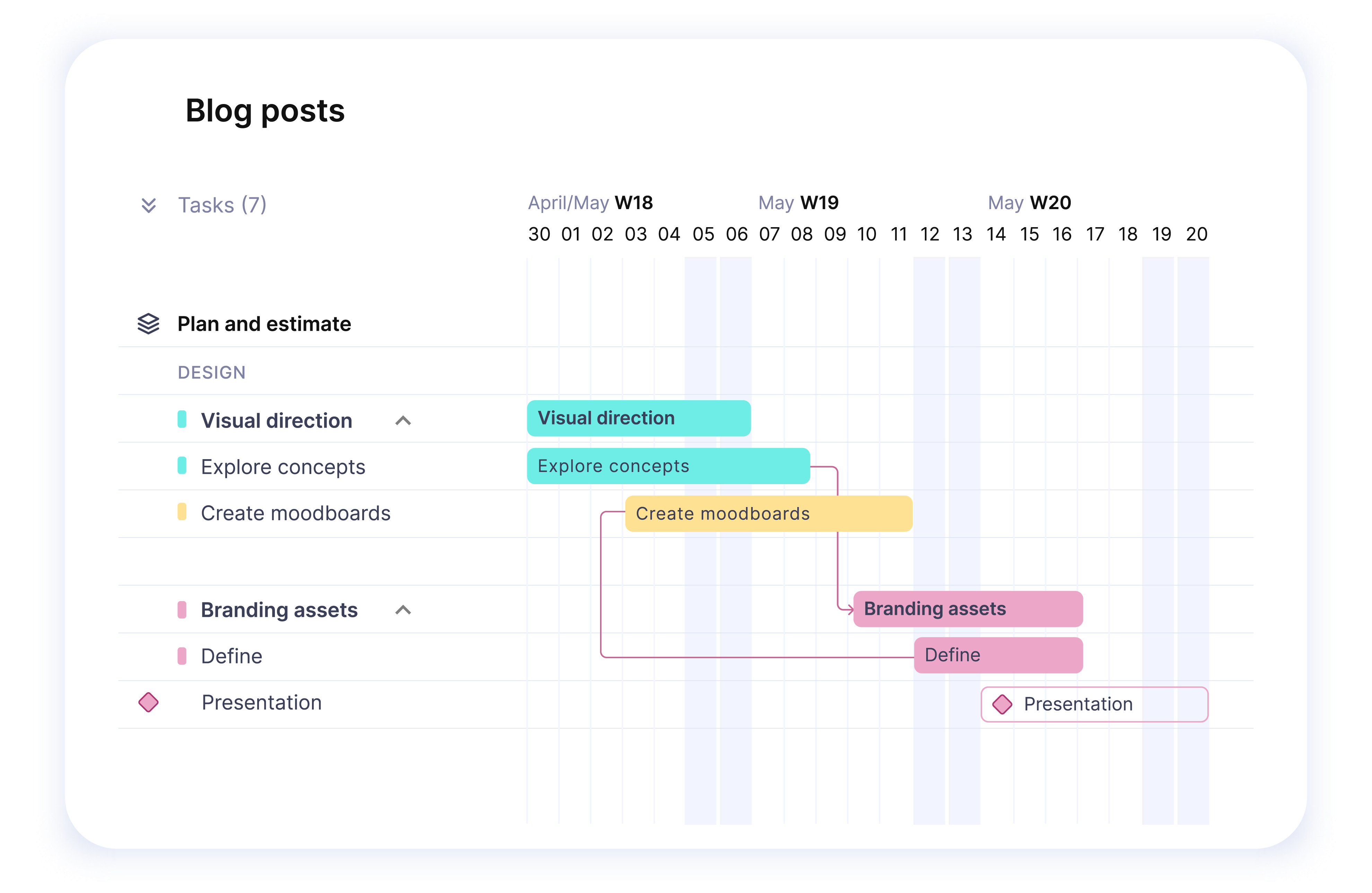
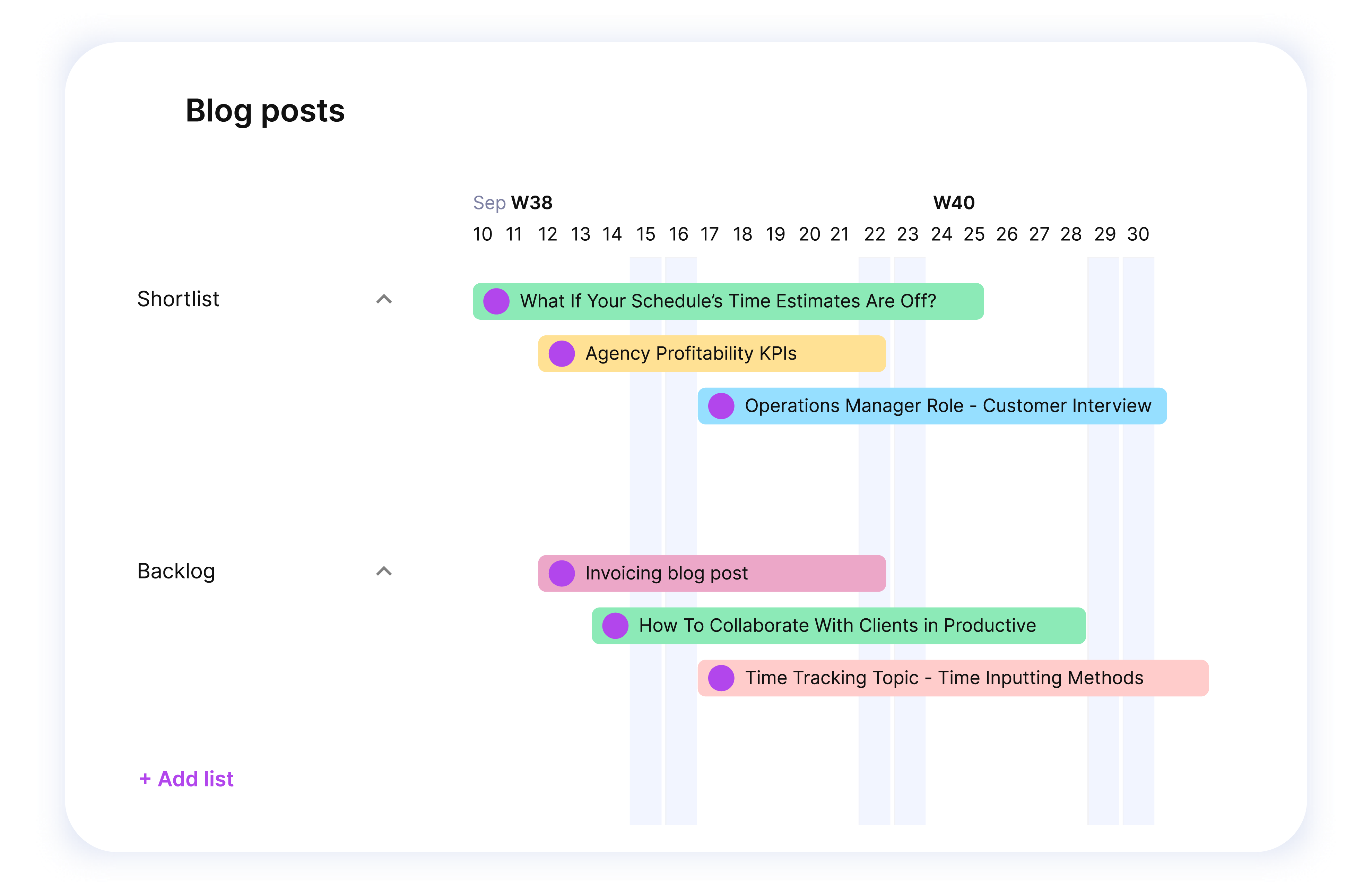
Track your progress through tasks, streamlined documentation, and a range of project formats. Dependencies and milestones provide a clear view of timelines and deliverables.

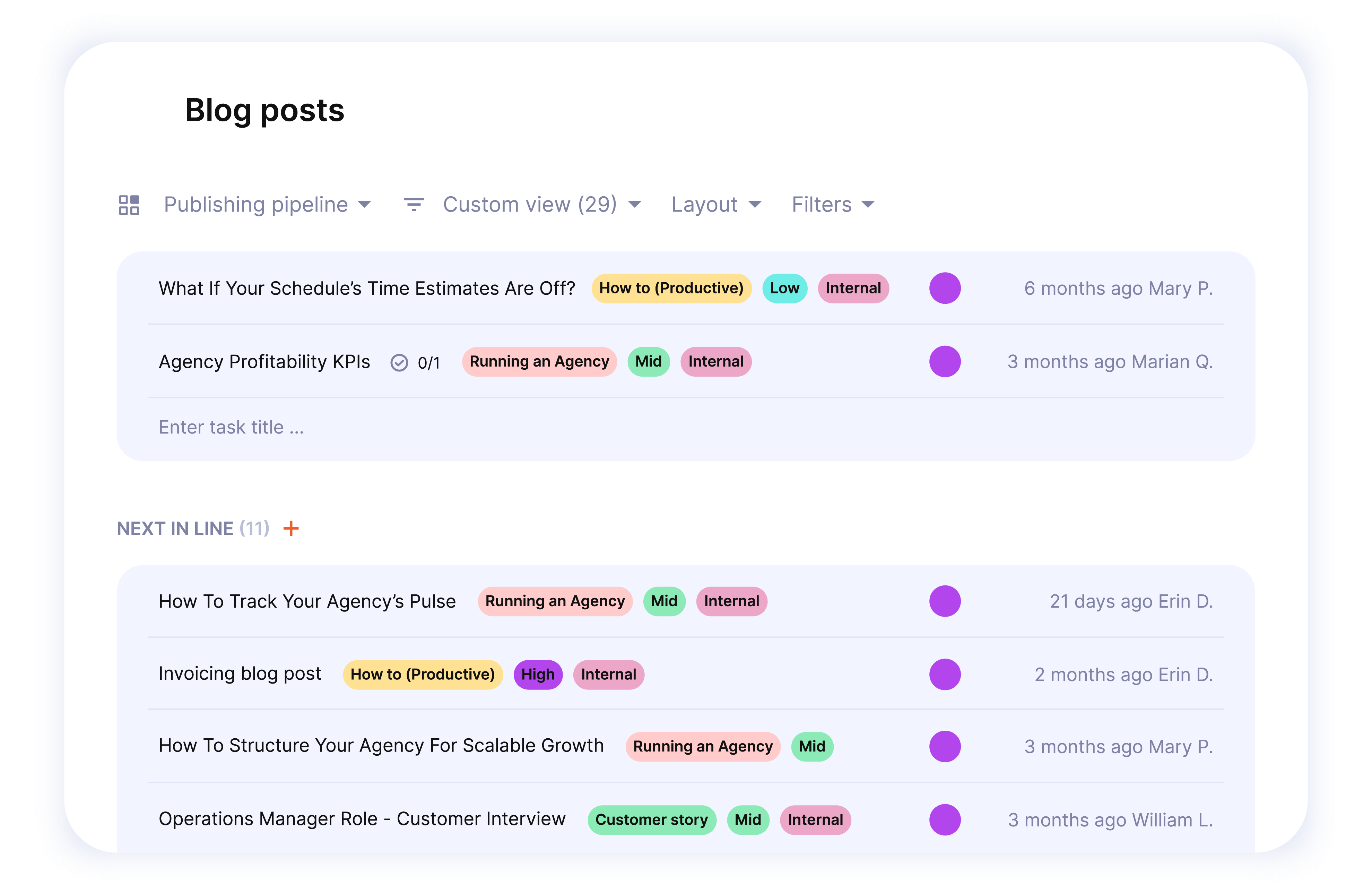
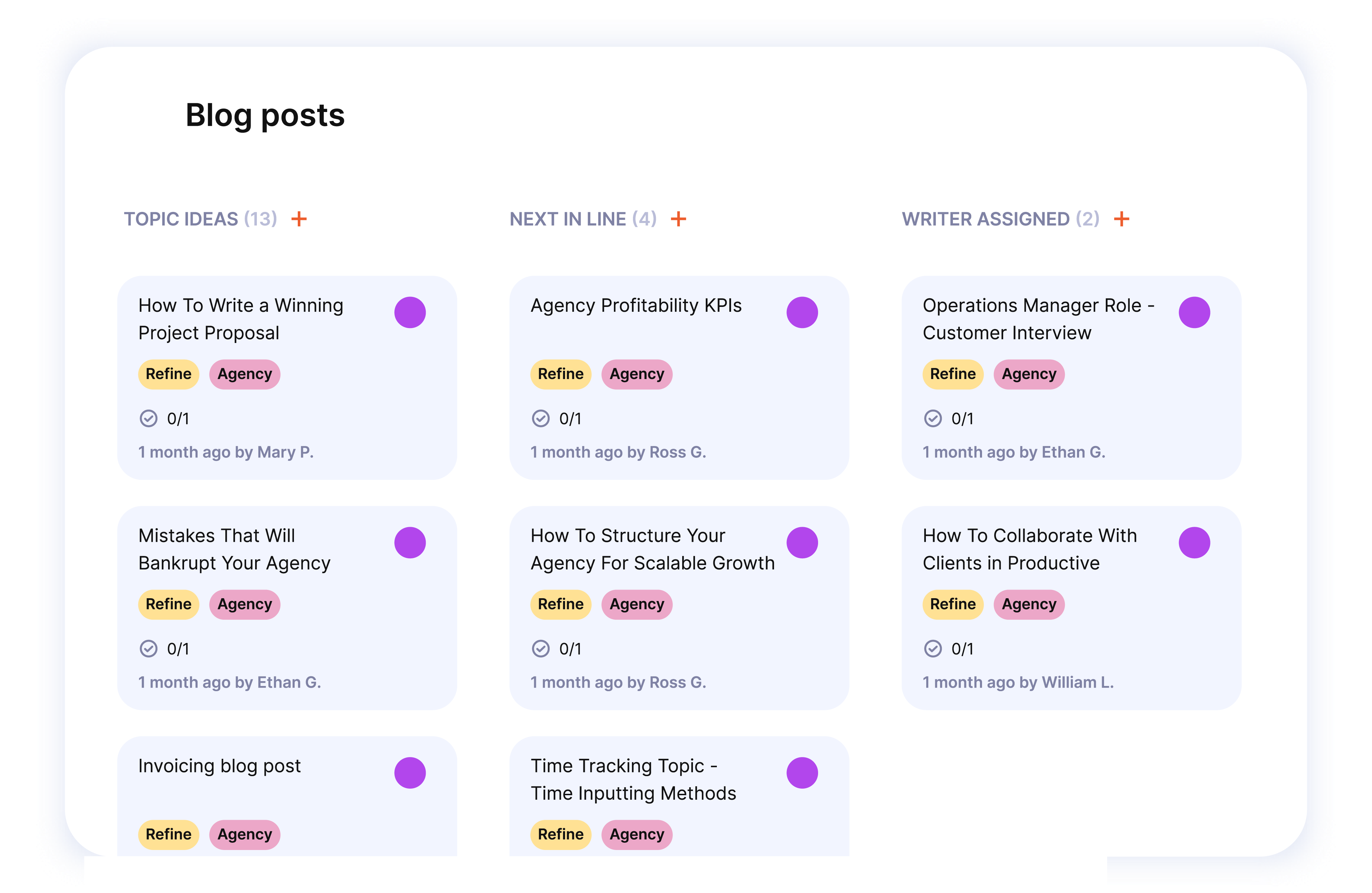
Customize a layout to manage your projects effectively
Design tailored views and collaborate them with your colleagues.
Consolidate Project Efforts for Your Entire Team
Involve team members, stakeholders, contractors, and clients in tasks—eliminate the need to manage project work across multiple platforms.
Nika Serdoner
Project Manager, ENKI
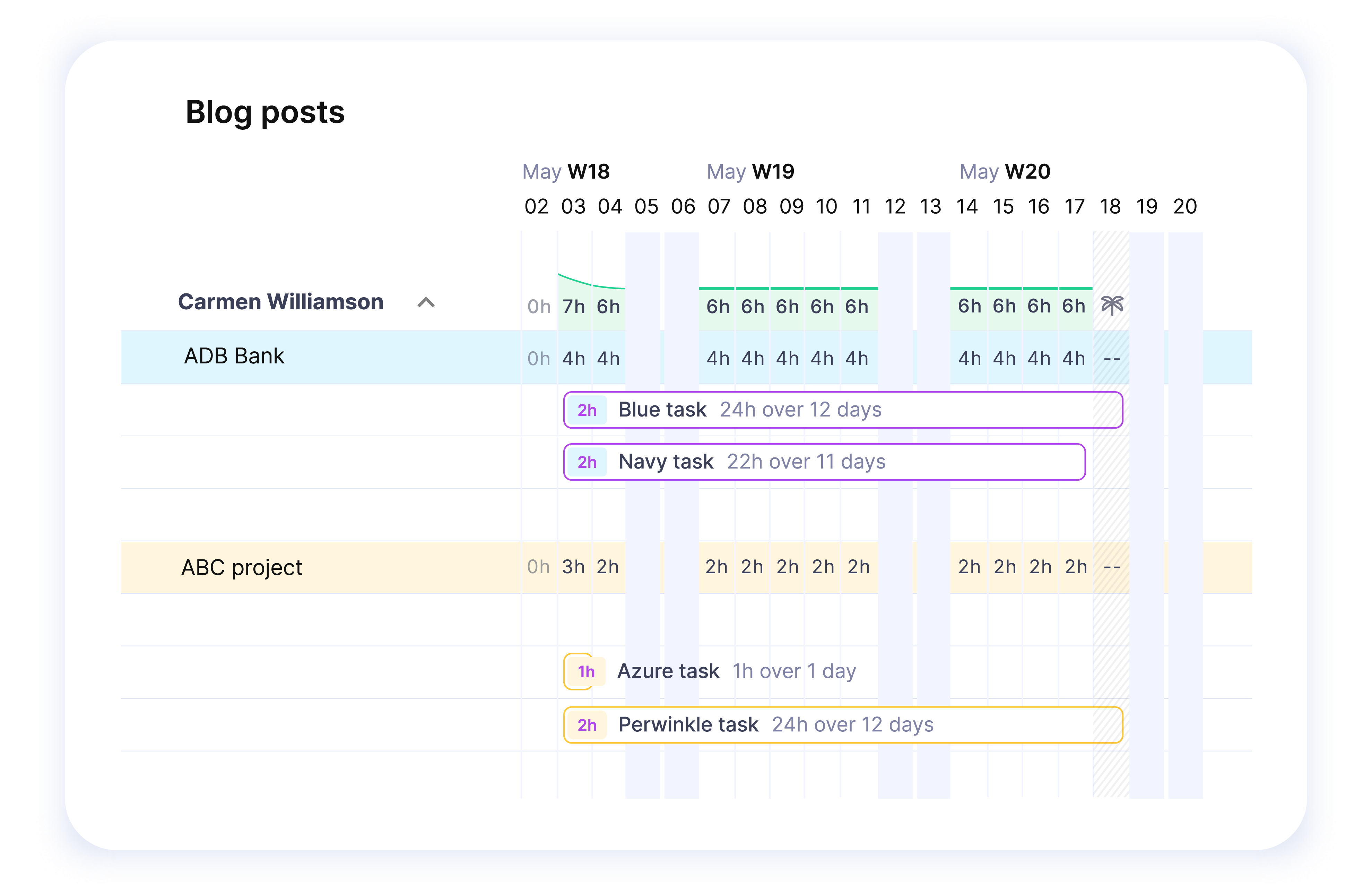
Having a thorough understanding of projects, current tasks, team availability, and profitability simplifies project management significantly.
Generate Documents Powered by AI and Collaborate